P-Valor: aprenda o que é e dicas de como aplicá-lo corretamente
O p-valor é uma probabilidade que nos ajuda a decidir se os resultados de um experimento ou análise são estatisticamente significativos.
Em termos mais simples, ele responde à pergunta: “Dado que a hipótese nula (de que não há diferença ou efeito) é verdadeira, qual é a probabilidade de observar dados tão ou mais extremos do que os dados que foram observados?”
Essa é uma ferramenta estatística amplamente utilizada, mas também frequentemente mal interpretada, o que pode levar a decisões incorretas.
Neste artigo, vamos entender o p-valor, mostrar como interpretá-lo corretamente e, claro, como evitar as armadilhas mais comuns que podem fazer você cair em ciladas estatísticas.
Afinal, o que é o p-valor?
O p-valor é a probabilidade de obtermos uma estatística de teste tão extrema (ou mais extrema) quanto a observada, dado que a hipótese nula é verdadeira.
Ele existe no contexto da inferência estatística, quando estamos analisando dados de uma amostra para tirar conclusões sobre uma população maior.
Imagine um cenário em que queremos testar se uma medicação funciona, se uma campanha de marketing gerou resultados expressivos ou se um novo algoritmo apresenta desempenho superior ao antigo.
Nesse contexto, o p-valor atua como um "termômetro": ele mede a probabilidade de observarmos os dados que coletamos (ou algo ainda mais extremo) se a hipótese nula, que postula a ausência de efeito ou diferença, for verdadeira.
De forma didática, podemos pensar que ele nos ajuda a avaliar se as diferenças encontradas entre as amostras são apenas fruto do acaso ou se refletem um efeito real.
E, sim, ele ajuda, mas não toma essa decisão. O p-valor apenas indica a probabilidade de o resultado observado ser obtido e deve ser sempre analisado junto a outras informações.
Para entender melhor sobre testes de hipóteses, leia nosso artigo Testes de hipóteses.
O p-valor em testes de hipóteses
Nos testes de hipóteses, analisamos dois cenários possíveis:
- H₀ ou hipótese nula: não há evidências estatísticas para afirmar que há efeito ou diferença.
- H1 ou hipótese alternativa: há evidências estatísticas suficientes para sugerir que há um efeito real.
Todo teste se inicia com a presunção de que a hipótese nula é verdadeira, isto é: de que não há efeito significativo. Com o teste, teremos evidências estatísticas para rejeitar ou não essa hipótese.
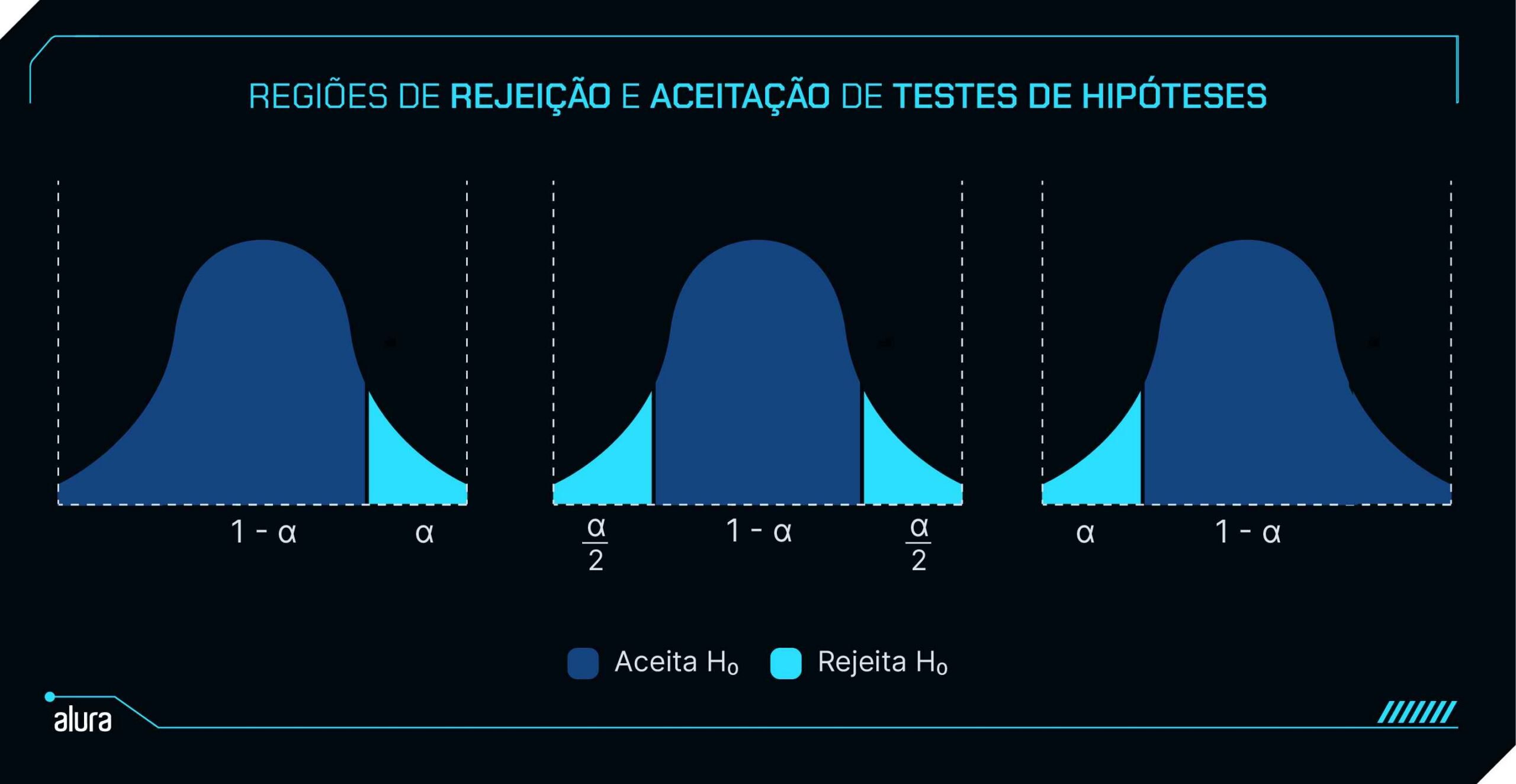
Utilizamos o nível de significância (α), um valor pré-estabelecido (geralmente 0,05), para comparar com o p-valor obtido.
- Se o p-valor ≤ α: Rejeitamos a hipótese nula.
- Se o p-valor > α: Não temos evidências suficientes para rejeitar a hipótese nula.
Nos testes bicaudais, rejeitamos H0 se o p-valor multiplicado por dois for menor que α. Já nos testes unicaudais, rejeitamos H0 se p-valor for menor que α em apenas uma extremidade da distribuição.
Na tabela abaixo, temos um exemplo de tomada de decisão de rejeição ou não da hipótese nula em uma situação de testes em duas versões de página web.
O que queremos saber é se há evidências estatísticas para afirmar que a versão B da página está trazendo mais cliques do que a versão A.
| p > 0.05 (Não Rejeita H₀) | p ≤ 0.05 (Rejeita H₀) | |
|---|---|---|
| Hipótese Nula (H₀) | Aceita-se a hipótese nula. | Rejeita-se a hipótese nula. |
| Exemplo | Não existem diferenças significativas na taxa de conversão entre a versão A e a versão B. | Rejeita-se a hipótese nula de que não há diferenças significativas na taxa de conversão entre as versões A e B. |
| Hipótese Alternativa (H₁) | Não existem evidências apontando para a hipótese alternativa. | Corrobora-se a hipótese alternativa. |
| Exemplo | Não há evidências estatísticas para afirmar que a versão B tenha uma taxa de conversão diferente da versão A. | Há evidências estatísticas para afirmar que a versão B tem uma taxa de conversão significativamente diferente da versão A. |
Matematicamente falando, a área de rejeição da hipótese nula estará abaixo da(s) extremidade(s) da curva de distribuição dos dados.
O ponto exato de divisão dessa região, que chamamos de região crítica, é definido pelo nível de significância α.

Como é o p-valor na prática
Imagine que estamos avaliando a eficácia de um novo medicamento para reduzir a pressão arterial.
Nosso objetivo é comparar a média de redução da pressão arterial entre dois grupos:
- Grupo 1: Pacientes que receberam o novo medicamento.
- Grupo 2: Pacientes que receberam um placebo.
Passo a passo do teste:
1 - Formulação das Hipóteses:
- H₀: O novo medicamento não difere do placebo na redução da pressão arterial.
- H1: O novo medicamento apresenta uma redução na pressão arterial diferente do placebo.
2 - Coleta dos Dados:
- Após o período de estudo, coletamos os dados de ambos os grupos e calculamos a média de redução da pressão arterial.
3 - Cálculo do p-valor:
- Aplicamos o teste estatístico (por exemplo, um teste t) para comparar as médias dos grupos e obtemos um p-valor.
4 - Decisão:
- Suponha que o p-valor calculado seja 0,03.
- Como 0,03 < 0,05 (nível de significância α), rejeitamos a hipótese nula e concluímos que há evidência estatística de que o novo medicamento tem um efeito na redução da pressão arterial.
- Se, ao contrário, o p-valor fosse 0,08, não rejeitaríamos H₀, pois 0,08 ≥ 0,05, indicando que não encontramos evidências estatísticas suficientes para afirmar que o novo medicamento é eficaz em comparação com o placebo.

O que o p-valor NÃO nos diz
Muitos erros de interpretação do p-valor acontecem por confusões em sua interpretação. Então, quando você for trabalhar com p-valor tenha em mente as seguintes ideias:
- Não é a probabilidade de que a hipótese nula seja verdadeira:: O p-valor indica a probabilidade de obter os dados observados (ou mais extremos) caso H₀ seja verdadeira, não a probabilidade de H₀ em si ser verdadeira.
- A probabilidade de a hipótese alternativa ser falsa: De forma similar, um p-valor baixo não garante, por si só, que a hipótese alternativa esteja correta em todos os aspectos.
- Não é uma medida do tamanho ou relevância do efeito: Mesmo com um p-valor muito baixo, o efeito real pode ser pequeno e, em termos práticos, irrelevante. Para analisar o tamanho do efeito, é importante acompanhar o p-valor com uma análise do tamanho do efeito.
- Não significa que tratamentos sem significância estatística não tenham efeito: Se o p-valor ultrapassar o limiar de 0,05, isso não quer dizer necessariamente que o novo tratamento não produz efeito algum. Em estudos com amostras pequenas, efeitos sutis podem não ser detectados mesmo quando são clinicamente relevantes.
- Valores-p próximos a 0,05 não indicam “tendência” para efeito:: Interpretar um p-valor de 0,06, por exemplo, como uma “quase significância” é inadequado. Um valor-p de 0,06 significa que há 6% de chance de se obter aquele resultado sob H₀, e, sendo o critério adotado é de 5%, não rejeita-se a hipótese nula
Armadilhas comuns
- P-Hacking: é a prática de manipular a coleta ou análise dos dados para encontrar resultados que sejam estatisticamente significativos, mesmo que, na realidade, não exista efeito.
- Multiplicidade de testes: quando vários testes são realizados, a chance de encontrar pelo menos um resultado significativo, por acaso, aumenta.
- Dogmatizar o nível de significância: o limite de alfa a 5% não deve ser rígido - essa é uma convenção, não uma verdade absoluta. Muitas vezes, um p-valor de 0,051 ou 0,049 não terá grande diferença prática. Um bom desenho experimental é essencial.
Conclusão
Compreender corretamente o p-valor – e o que ele não representa – é essencial para evitar conclusões precipitadas.
A estatística não é uma ferramenta infalível, mas, quando usada com discernimento, permite tomar decisões mais embasadas.
Para isso, é importante combinar o p-valor com uma análise crítica do contexto, do tamanho do efeito e do desenho experimental.
Se você deseja aprender mais sobre testes de hipóteses e tomada de decisão com p-valor, confira nossas formações em estatística:
Esses cursos apresentam ferramentas estatísticas essenciais de forma direta e prática, te capacitando a tomar decisões coerentes e com embasamento.
Um abraço, pessoal. E bons estudos!












